在做行测数量联系标题时经常会遇到一元二次函数，如求解、求极值等，其间调查求极值的标题相对会更多一些。尽管这是中学阶段学过的知识点，但不少同学们有所忘记。那么接下来，就带着我们一同回忆一下一元二次函数求极值的三种常用办法，一块儿来看看吧!

  一般地，把形如y=ax+bx+c(a0)(a、b、c是常数)的函数叫做二次函数，其间a称为二次项系数，b为一次项系数，c为常数项。图象为左右对称的抛物线时，抛物线开口向上，有最小值，图象如下：

  y=ax+bx+c(a0)，一元二次函数在图象对称轴

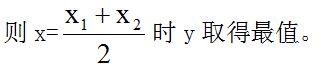
  将一元二次函数收拾为y=a(x-x1)(x-x2)的方式，在函数图象与x轴有两个交点的情况下，可先求出y=0时x的两个值x1和x2，

  将一元二次函数收拾为y=a(m+x)(n-x)的方式。因(m+x)与(n-x)之和为定值，依据均值不等式原理，当且仅当m+x=n-x时，y取得最值。

  例.某电脑商城出售10种价格档位的电脑。最低价格档位的电脑每月可售出120台，每台可获利160元。每提高一个价格档位，则月销售量就会削减10台，但单台赢利可增加40元。若某月该电脑商城只出售某一种价格档位的电脑，则当月可取得的最大赢利是( )元。

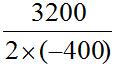
  【解析】B。办法一，设该月售出电脑的价格档位比最低价格档位高x个档位，则该月可售出(120-10x)台电脑，每台获利(160+40x)元。当月可取得的赢利为(160+40x)×(120-10x)=-400x2+3200x+19200,当x=-=4时取得的赢利最多，最大赢利为(160+40×4)×(120-10×4)=320×80=25600元。故本题选B。

  办法三，设该月售出电脑的价格档位比最低价格档位高x个档位，则该月可售出(120-10x)台电脑，每台获利(160+40x)元。当月可取得的赢利为(160+40x)×(120-10x)=400(4+x)×(12-x)。依据均值不等式原理，当且仅当4+x=12-x，即x=4时，取得的赢利最多，最大赢利为(160+40×4)×(120-10×4)=320×80=25600元。故本题选B。

  期望经过以上标题的沟通，能让各位同学根本把握一元二次函数求极值的三种常用办法。你们能够在备考中多多操练该种类型的标题，以熟练把握解题办法。